B 트리
IT 위키
- Balanced Tree, B-Tree, B Tree
1 개요[편집 | 원본 편집]
- 자가 균형 트리(Self Balancing Tree)[1]의 일종.
2 구성[편집 | 원본 편집]
- 키(key): 검색을 하기 위한 키
- 포인터의 개수보다 하나가 더 많음
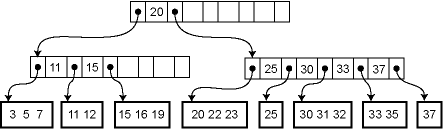
- 양쪽에 포인트를 두고 있는 구조 (위 그림 참고)
- 포인터(pointer): 자식 노드의 주소를 가리킴
- 노드: 두 종류로 크게 나뉜다.
- 내부 노드(internal nodes): 리프 노드를 제외한 노드들은 결국 리프 노드를 검색하기 위한 용도로 쓰인다.
- 리프 노드(leaf node): 실제 데이터를 담고 있는 노드
3 조건[편집 | 원본 편집]
차수가 m인 B 트리는 아래의 조건을 만족해야 한다.
- 모든 노드는 최대 m개의 자식들을 가진다.
- 루트노드와 리프노드가 아닌 모든 노드는 최소 m/2개의 자식을 가진다.
- 루트노드는 2개 이상의 자식을 가진다.
- k개의 자식을 가진 노드는 k-1개의 키를 가진다.
- 즉, 자식을 가진 노드는 최소 m/2-1개에서 최대 m-1개의 키를 가진다.
- 모든 리프노드들은 같은 높이에 있어야 한다.
- 모든 노드들은 키와 자식노드에 대한 포인터로 이루어져 있다.
4 특징[편집 | 원본 편집]
- 탐색 시간 복잡도 : O(logN)
- 노드의 삽입 또는 삭제 연산 후에도 정렬된 자료구조를 보장한다.
5 비트리의 장단점[편집 | 원본 편집]
| 장점 | 단점 |
|---|---|
|
|
6 B 트리 연산[편집 | 원본 편집]
6.1 1. 삽입 (Insertion)[편집 | 원본 편집]
- 적절한 리프 노드를 찾아 삽입한다.
- 노드가 초과(m개의 키)되면 중앙 키를 상위 노드로 올리고, 노드를 분할한다.
6.2 2. 삭제 (Deletion)[편집 | 원본 편집]
- 삭제 후 노드에 남아 있는 키 개수를 확인한다.
- 최소 키 개수보다 적으면 형제 노드에서 빌리거나, 병합을 수행한다.
6.3 3. 검색 (Search)[편집 | 원본 편집]
- 루트에서 시작하여 적절한 자식 노드를 따라가며 키를 찾는다.
- O(log n)의 시간 복잡도로 검색 가능하다.
7 B 트리 구현 (Python)[편집 | 원본 편집]
class BTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.keys = []
self.children = []
class BTree:
def __init__(self, t):
self.root = BTreeNode(True)
self.t = t # 최소 차수
def search(self, node, key):
i = 0
while i < len(node.keys) and key > node.keys[i]:
i += 1
if i < len(node.keys) and key == node.keys[i]:
return node
if node.leaf:
return None
return self.search(node.children[i], key)
def insert(self, key):
root = self.root
if len(root.keys) == (2 * self.t) - 1:
new_root = BTreeNode(False)
new_root.children.append(self.root)
self.split_child(new_root, 0)
self.root = new_root
self.insert_non_full(new_root, key)
else:
self.insert_non_full(root, key)
def insert_non_full(self, node, key):
i = len(node.keys) - 1
if node.leaf:
node.keys.append(None)
while i >= 0 and key < node.keys[i]:
node.keys[i + 1] = node.keys[i]
i -= 1
node.keys[i + 1] = key
else:
while i >= 0 and key < node.keys[i]:
i -= 1
i += 1
if len(node.children[i].keys) == (2 * self.t) - 1:
self.split_child(node, i)
if key > node.keys[i]:
i += 1
self.insert_non_full(node.children[i], key)
def split_child(self, node, i):
t = self.t
y = node.children[i]
z = BTreeNode(y.leaf)
node.keys.insert(i, y.keys[t - 1])
node.children.insert(i + 1, z)
z.keys = y.keys[t:(2 * t - 1)]
y.keys = y.keys[0:(t - 1)]
if not y.leaf:
z.children = y.children[t:(2 * t)]
y.children = y.children[0:t]
def traverse(self, node):
for i in range(len(node.keys)):
if not node.leaf:
self.traverse(node.children[i])
print(node.keys[i], end=" ")
if not node.leaf:
self.traverse(node.children[len(node.keys)])
# B 트리 테스트
btree = BTree(3) # 최소 차수 t = 3
for key in [10, 20, 5, 6, 12, 30, 7, 17]:
btree.insert(key)
print("B 트리 순회 결과:")
btree.traverse(btree.root)
print("\n")
8 같이 보기[편집 | 원본 편집]
9 각주[편집 | 원본 편집]
- ↑ 모든 리프노드의 높이를 항상 같게 유지하는 트리